Soma de Riemann
Soma de Riemann consiste em se fazer uma aproximação da área delimitada por uma função, curva ou gráfico através de retângulos, quando da utilização de uma expressão, tal como, Σ f(x)*Δx. Esse raciocínio é devido em homenagem ao matemático alemão Bernhard Riemann.
Tal soma é dada pela divisão da região a ser calculada em retângulos que, juntos, formam uma região bem próxima àquela a ser medida. Ou seja, calcula-se a área de cada retângulo e soma-se todas essas áreas juntas para aproximar ao valor de área pretendido para a função em questão.
Tendo em vista que a região preenchida por retângulos, geralmente não corresponde a exata forma da região a ser medida, a Soma de Riemann será diferente desta. Isso ocorre quando o número de partições do intervalo de definição da função for um número inteiro (finito). Esse erro, determinado pela soma de Riemann e a área exata da função, pode ser reduzido se a região for cada vez mais dividida, usando retângulos com bases cada vez menores, e à medida em que esse número se torna cada vez maior, o erro fica cada vez menor. Intuitivamente propomos a ilustração a seguir, quando fazemos uma partição inicial em sete partes num determinado intervalo [a,b], dentro do domínio da função, onde desejamos avaliar a área da mesma:
Fonte: Regina Lúcia Quintanilha de Lima & Murilo Ferreira Yamamoto. In: http://www.uff.br/webmat/, 2003.
Encontramos em livros-textos, livros-didáticos e em materiais de auxílio à disciplinas de Cálculo Integral, três tipos principais de Somas de Riemann. Tais somas são classificadas dependendo de cada ponto que é escolhido para se determinar as alturas dos retângulos das partições do intervalo de definição da função:
- Soma à Direita - SD: o ponto final à direita do subsegmento;
- Soma à Esquerda - SE: o ponto final à esquerda do subsegmento;
- Soma ao Ponto Médio - SPM: o caminho do meio, ou intermediário, entre os pontos extremos do sub-intervalo;
Entretanto, propomos que seja verificada, após o estudo, através da resolução dos problemas propostos, a equivalência entre esses três tipos de Somas de Riemann.
Para adentrarmos efetivamente na constituição desse conhecimento, definiremos a Soma de Riemann da seguinte forma:
Seja, inicialmente, f uma função contínua num intervalo [a,b] e, sem perda de generalidade, tal que  para todo
para todo 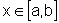 .
.
 para todo
para todo 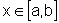 .
.
Para calcularmos a área delimitada pela região compreendida entre o gráfico da função f e o eixo Ox, quando x varia no intervalo  , devemos considerar uma partição do intervalo
, devemos considerar uma partição do intervalo  , tal qual aquela determinada pelo conjunto de pontos
, tal qual aquela determinada pelo conjunto de pontos  .
.
 , devemos considerar uma partição do intervalo
, devemos considerar uma partição do intervalo  , tal qual aquela determinada pelo conjunto de pontos
, tal qual aquela determinada pelo conjunto de pontos  .
.
Assim, apresentamos n sub-intervalos, em que, cada um deles se apresenta na forma  , onde o índice i varia de 1 até n, ou seja,
, onde o índice i varia de 1 até n, ou seja,  . Se as n divisões daquele intervalo forem todas do mesmo tamanho, teremos cada um dos sub-intervalos com comprimento
. Se as n divisões daquele intervalo forem todas do mesmo tamanho, teremos cada um dos sub-intervalos com comprimento  , onde
, onde  .
.
 , onde o índice i varia de 1 até n, ou seja,
, onde o índice i varia de 1 até n, ou seja,  . Se as n divisões daquele intervalo forem todas do mesmo tamanho, teremos cada um dos sub-intervalos com comprimento
. Se as n divisões daquele intervalo forem todas do mesmo tamanho, teremos cada um dos sub-intervalos com comprimento  , onde
, onde  .
.
Nesses sub-intervalos  , podemos considerar um ponto arbitrário mi, que poderá satisfazer, qualquer um dos 5 tipos de soma de Riemann, como apresentamos acima. Logo, obteremos um valor aproximado para a área da região, que representado por (BARUFI et al.):
, podemos considerar um ponto arbitrário mi, que poderá satisfazer, qualquer um dos 5 tipos de soma de Riemann, como apresentamos acima. Logo, obteremos um valor aproximado para a área da região, que representado por (BARUFI et al.):
 , podemos considerar um ponto arbitrário mi, que poderá satisfazer, qualquer um dos 5 tipos de soma de Riemann, como apresentamos acima. Logo, obteremos um valor aproximado para a área da região, que representado por (BARUFI et al.):
, podemos considerar um ponto arbitrário mi, que poderá satisfazer, qualquer um dos 5 tipos de soma de Riemann, como apresentamos acima. Logo, obteremos um valor aproximado para a área da região, que representado por (BARUFI et al.):
que será a Soma de Riemann relativa à partição P e à função f.
Ao tomarmos o limite pela partição do intervalo [a,b], fazendo crescer indefinidamente o número de pontos dessa partição, ou seja, fazendo o número de partições , obteremos para qualquer escolha dos pontos xi* em cada um dos sub-intervalos
, obteremos para qualquer escolha dos pontos xi* em cada um dos sub-intervalos  , para
, para  , qualquer um dos três tipos de somas acima, na forma
, qualquer um dos três tipos de somas acima, na forma  , é denominada soma de Riemann para a função f, relativa à partição P e aos números xi*, para
, é denominada soma de Riemann para a função f, relativa à partição P e aos números xi*, para  .
.
Ao tomarmos o limite pela partição do intervalo [a,b], fazendo crescer indefinidamente o número de pontos dessa partição, ou seja, fazendo o número de partições
 , obteremos para qualquer escolha dos pontos xi* em cada um dos sub-intervalos
, obteremos para qualquer escolha dos pontos xi* em cada um dos sub-intervalos  , para
, para  , qualquer um dos três tipos de somas acima, na forma
, qualquer um dos três tipos de somas acima, na forma  , é denominada soma de Riemann para a função f, relativa à partição P e aos números xi*, para
, é denominada soma de Riemann para a função f, relativa à partição P e aos números xi*, para  .
.
Destacamos que a escolha da partição determina o tamanho de  , para
, para  , e por esse motivo, indicaremos a soma de Riemann, relativa à função f, pela expressão:
, e por esse motivo, indicaremos a soma de Riemann, relativa à função f, pela expressão:
 , para
, para  , e por esse motivo, indicaremos a soma de Riemann, relativa à função f, pela expressão:
, e por esse motivo, indicaremos a soma de Riemann, relativa à função f, pela expressão: .
.
Logo, nos advém a definição usual de área, ou integral, definida por uma função num intervalo [a,b], onde

Atentamos ao fato de que tal área será igual ao limite da soma das áreas dos n retângulos, quando o número desses retângulos tende a infinito.
Abaixo deixamos dois links para o leitor estudar e inferir os resultados discutidos e poder compreender de uma maneira mais visual os conceitos matemáticos que fundamentaram/fundamentam nossa proposta:
Uma outra formalização dos conceitos das Somas de Riemann podem ser encontradas em Revista Unión como um trabalho de pesquisa dos autores desse blog.
Uma outra formalização dos conceitos das Somas de Riemann podem ser encontradas em Revista Unión como um trabalho de pesquisa dos autores desse blog.
- Somas de Riemann à direita, à esquerda e por pontos médios (Créditos de Renato Francisco Lopes Mello in GeoGebraTube).
- Soma de Riemann continuação (Créditos de Luis Cláudio LA in GeoGebra).
Referências Bibliográficas:
BARUFI, M. C. B., et al.. Soma de Riemann. Disponível em: <http://ecalculo.if.usp.br/>. Acesso em 01/09/2015.
LIMA, L. Q.; YAMAMOTO, M. F.. Soma de Riemann. Disponível em: <http://www.uff.br/webmat/Calc1_LivroOnLine>. Acesso em 02/09/2015.
BOULOS, Paulo. Introdução ao Cálculo. São Paulo: Edgard Blücher Ltda, 1974.
BOYER, Carl B. Cálculo. São Paulo: Atual, 1996.
GUIDORIZZI, Hamilton L. Um curso de Cálculo. Rio de Janeiro: LTC, 1998.
HUGHES, Deborah, GLEASON, Andrew M. Cálculo - Volume 1. Rio de Janeiro: LTC, 1997.
LEITHOLD, Louis. Cálculo com geometria analítica. Tradução: Cyro de Carvalho Patarra. São Paulo: Harbra, 1994.
SIMMONS, George F. Cálculo com Geometria Analítica. Tradução: Seiji Hariki. São Paulo: McGraw-Hill, 1987.
STEWART, James. Calculus. Tradução: Cyro de Carvalho Patarra et al. São Paulo: Pioneira Thomson Learning, 2001.
SWOKOWSKI, Earl W. Cálculo com Geometria Analítica. Tradução Alfredo Alves de Faria. São Paulo: Makron Books, 1994.
THOMAS, George B. Cálculo - Volume 1. Tradução: Paulo Boschcov. São Paulo: Pearson Education do Brasil, 2002.


Nenhum comentário:
Postar um comentário