Numa pesquisa a livros didáticos pudemos constatar que grande parte deles não introduz mais o conceito de integração através de Soma de Riemann. E, se o faz, é de maneira lacônica, onde o estudantes sequer pode inferir e conectar a ideias e problemas geradores de um novo conceito. A conexão e a potencialização da aprendizagem dos mesmos sobre a construção dessa ferramenta do Cálculo Integral é perdida, e passa a ser percebida como um conteúdo a mais para ser trabalhado, ou que não há a menor conexão com a utilidade das ferramentas usuais para se calcular a área abaixo de uma curva/função.
Na postagem sobre Soma de Riemann: Teoria, Exemplos e Reflexões, elencamos os livros didáticos que nos dispusemos a analisar. Foi quando percebemos que poucos trazem a abordagem de soma de Riemann como conceito introdutório ao cálculo de áreas, ou integração definida. A maioria parte direto para a definição de integral por meio de funções primitivas, seguidas de regras de integração. O que, ao nosso ver, causa muitos problemas, enquanto um construto mal fundamentado e totalizante, que não fora/ nem será abordado de uma maneira efetiva, em que o estudante possa entender, compreender e relacionar-se com aqueles signos.
Sendo assim, tentando subverter este modelo superficial de introdução à integração, expomos aqui, o que nos motivou a trabalhar com o tema, e nos dedicamos ao estudo e proposta de trabalho sobre a Soma de Riemann como meio de introdução à Integração.
Buscamos suporte em tecnologias informacionais para esta introdução, mais especificamente, em um software de Geometria Dinâmica junto ao blog aqui construído. Justificamos a tecnologia enquanto fundo para esta abordagem pois com ela é possível a visualização dos conceitos e da construção de modos distintos de outras abordagens sem a mesma, modos que consideramos abrir possibilidades para os processos intuitivos, que corroboram muitas vezes à descoberta, ao novo, inclusive a novas formas de compreender que a complexidade empregada por muitos no que diz respeito ao cálculo, é acessível se trabalhada junto metodologias que contemplam tecnologias informáticas.
A potencialidade das tecnologias, quando focada junto ao ensino e à aprendizagem de Matemática, nos motivou a pensar uma proposta de Introdução à Integração através de Soma de Riemann utilizando o Software Geogebra, no qual, a questão da visualidade que se mostra uma dificuldade em muitas situações, pode ser melhor tratada visto que o software fornece ferramentas que facilitam a construção de gráficos que são muitas vezes inviáveis de construir sem o auxílio do computador.
A seguir destacamos dois trabalhos divulgados em meio acadêmico que abordam o tema com propriedade e que foram base para nossos estudos:
Na postagem sobre Soma de Riemann: Teoria, Exemplos e Reflexões, elencamos os livros didáticos que nos dispusemos a analisar. Foi quando percebemos que poucos trazem a abordagem de soma de Riemann como conceito introdutório ao cálculo de áreas, ou integração definida. A maioria parte direto para a definição de integral por meio de funções primitivas, seguidas de regras de integração. O que, ao nosso ver, causa muitos problemas, enquanto um construto mal fundamentado e totalizante, que não fora/ nem será abordado de uma maneira efetiva, em que o estudante possa entender, compreender e relacionar-se com aqueles signos.
Sendo assim, tentando subverter este modelo superficial de introdução à integração, expomos aqui, o que nos motivou a trabalhar com o tema, e nos dedicamos ao estudo e proposta de trabalho sobre a Soma de Riemann como meio de introdução à Integração.
Buscamos suporte em tecnologias informacionais para esta introdução, mais especificamente, em um software de Geometria Dinâmica junto ao blog aqui construído. Justificamos a tecnologia enquanto fundo para esta abordagem pois com ela é possível a visualização dos conceitos e da construção de modos distintos de outras abordagens sem a mesma, modos que consideramos abrir possibilidades para os processos intuitivos, que corroboram muitas vezes à descoberta, ao novo, inclusive a novas formas de compreender que a complexidade empregada por muitos no que diz respeito ao cálculo, é acessível se trabalhada junto metodologias que contemplam tecnologias informáticas.
A potencialidade das tecnologias, quando focada junto ao ensino e à aprendizagem de Matemática, nos motivou a pensar uma proposta de Introdução à Integração através de Soma de Riemann utilizando o Software Geogebra, no qual, a questão da visualidade que se mostra uma dificuldade em muitas situações, pode ser melhor tratada visto que o software fornece ferramentas que facilitam a construção de gráficos que são muitas vezes inviáveis de construir sem o auxílio do computador.
A seguir destacamos dois trabalhos divulgados em meio acadêmico que abordam o tema com propriedade e que foram base para nossos estudos:
- O USO DO SOFTWARE GEOGEBRA EM CÁLCULO ANÁLISE GRÁFICA DE DERIVADA E INTEGRAL (Créditos de TRINDADE; WANGHON, 2011).
- Soma de Riemann e cálculo de área sob uma curva por integrais com auxílio do software Geogebra (Créditos de SILVA; PEREIRA, DAMIN; YONEZAWA, 2014).



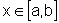
 ,
, 
 , onde o índice i varia de 1 até n, ou seja,
, onde o índice i varia de 1 até n, ou seja,  . Se as n divisões daquele intervalo forem todas do
. Se as n divisões daquele intervalo forem todas do  , onde
, onde  .
. , podemos considerar um ponto arbitrário mi, que poderá satisfazer, qualquer um dos 5 tipos de soma de Riemann, como apresentamos acima. Logo, obteremos um valor aproximado para a área da região, que representado por (BARUFI et al.):
, podemos considerar um ponto arbitrário mi, que poderá satisfazer, qualquer um dos 5 tipos de soma de Riemann, como apresentamos acima. Logo, obteremos um valor aproximado para a área da região, que representado por (BARUFI et al.):





 , para
, para  , e por esse motivo, indicaremos a soma de Riemann, relativa à função f, pela expressão:
, e por esse motivo, indicaremos a soma de Riemann, relativa à função f, pela expressão: .
.